傅里叶变换是一种数学工具，用于将一个函数从时间域（或空间域）转换到频率域。它是一种分析信号的方法，可将信号分解成不同频率的成分，从而使我们能够理解信号的频谱特性。傅里叶变换在许多领域广泛应用，包括信号处理、图像处理、音频处理、通信等。

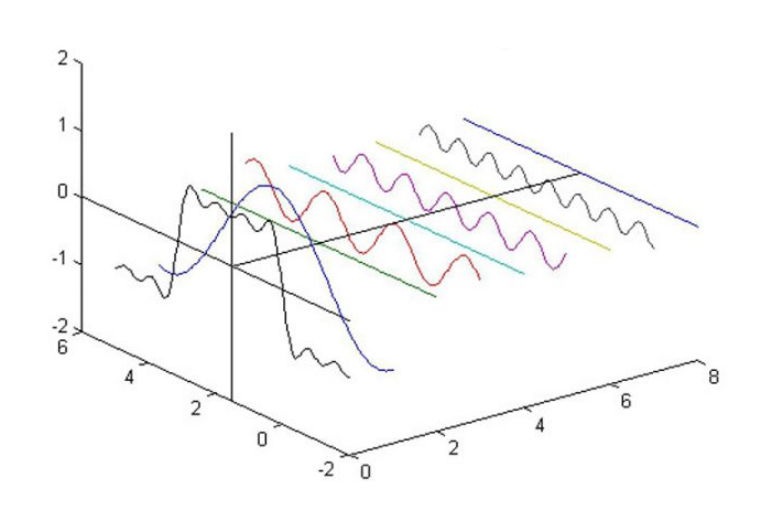
下面是一个简单的示例来说明傅里叶变换的概念：

假设有一个连续的周期性信号，如下所示：

f(t) = cos(2πft)

其中，f(t) 是关于时间 t 的信号，cos 表示余弦函数，f 是信号的频率，2π 是一个常数。

现在，我们可以使用傅里叶变换来将这个信号从时间域转换到频率域。傅里叶变换的公式如下：

F(ω) = ∫[0, T] f(t) * e^(-iωt) dt

其中，F(ω) 是信号在频率域中的表示，ω 是频率，i 是虚数单位，t 是时间，f(t) 是时间域中的信号。

对于我们的示例信号 f(t) = cos(2πft)，我们可以进行傅里叶变换：

F(ω) = ∫[0, T] cos(2πft) * e^(-iωt) dt

这个积分将会给出一个包含频率信息的复数函数 F(ω)。这个函数将告诉我们原始信号中包含的频率成分及其幅度。在这种情况下，傅里叶变换将产生两个脉冲，一个在频率 f 上，另一个在频率 -f 上，其振幅分别为 0.5。这表明原始信号是一个包含频率为 f 的余弦波。

傅里叶变换的一个重要应用是在信号处理中，它可以帮助我们分析信号的频谱特性，过滤特定频率的噪声或信号成分，以及在通信中调制和解调信号。它也用于图像处理和音频处理，以进行频域分析和处理。